在電腦還沒發明以前,人類用10進位的算術,建立了龐大的科學知識,數學、物理、化學、生物學、醫學……。在研究各項科學時,科學家需要進行大量的計算,來證明自己的「假設」是正確的,這是電腦在科學上可能的用途。
至於一般的商業行為上,運算的「份量」可能沒有這麼龐大,但是商業行為牽涉到「金錢」的往來,貨幣的交易與輸送……,需要的是「極端精確」的計算。同樣地,商人也需要電腦,以達成「精確算錢」的目的。
2進位的電腦比較容易設計與製造
所以,無論你是要進行「8 + 5 = 13」這樣的簡單加法,還是要進行8×6.02×1023這樣的科學運算,總之你需要一臺電腦。有了電腦,各種運算就能快速精確。
在此我先複習一下講解過的邏輯概念。
概念上是:數字只是用來代替數值的符號,而數值是抽象的概念。當我們進行各種數學運算時,實際上是利用符號來表達數值的變化。因此,能用10進位進行數學運算,那用2進位也一樣可以做,而且運算的準確度並無二致。
既然人類明明是習慣使用10進位,那為何要麻煩去改用2進位?這只是因為,我們要設計電腦,使用電子裝置來進行「2進位數學運算」會比較容易。如果要使用電子裝置來直接做「10進位數學運算」,那電腦幾乎不可能被設計出來,因為那種電路太複雜、太難設計了。要用電子元件模擬出數學演算,目前人類只能使用2進位的設計。
為什麼不用3進位?4進位?不為什麼,因為那都沒有必要,且一樣會增加設計上的困難度。
總之,經過了長時間的演化與嘗試,電腦得使用2進位的設計,這件事已經被確定了。
2進位的加法
好,底下我們來示範,什麼是「2進位加法」。2進位系統中,只用「0和1」來表示數字,逢2進1,所以才被稱為「2進位」。底下4個算式,用來示範「單一bit的2進位數字相加」(請注意:底下的示範都只使用2進位數字,所以就不標註基底了):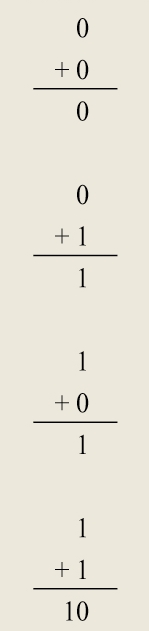
關鍵在於「1 + 1」的部份。「1 + 1 = 10」是2進位算法,此時要進1。如果能夠理解,接著我們來做一道3位數加法:「101 + 111」: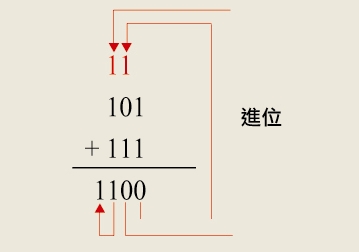
是不是很容易?「101 + 111 = 1100」,簡單透了!但是,1 + 1此時不等於2而等於10,這時要記得寫0進1。所以,你得非常注意,真正的加法運算其實不只是是「兩個數字相加」,一個完整的「2個數字相加時」,實際上我們得做的常常是「3個數字相加」──因為我們得考慮進位。
完整的加法運算需考慮「進位」這件事
再強調一遍:要設計一臺電腦做「2個數值的2進位加法」,關鍵在於:
● 單一位元的加法,實際上要做的是「3個數值的相加」而不只是「2個」數值的相加,因為要考慮「進位」的問題。
● 雖然單一位元的加法只能處理很簡單,很小的數值的運算(就一個bit而已),但是只要把此功能串連起來,2位元加法、3位元加法?……16位元加法?32位元加法?在「複雜度許可」的範圍內,只要能做出單一位元的加法功能,要做出更長的加法,其實只是相同功能元件的串連延伸而已。
所以,我們要想像一個「加法器」有加法的功能。怎麼設計?先不要管,暫時假設這一個「1位元加法器」只是「黑盒子」,能執行加法的功能。在此先用文字來描述這個1位元加法器,並把1位元加法器分為「不考慮進位」的簡單版,和「要考慮進位」的正確版:
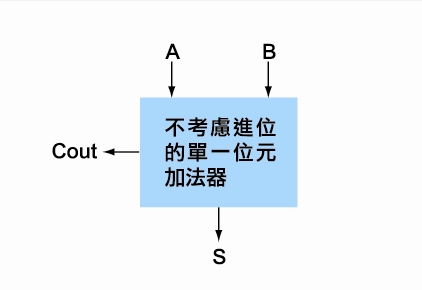
不考慮進位的1位元加法器
會有2個輸入,4種可能性:0 + 0,0 + 1,1 + 0或1 + 1,2個輸出結果,也是4種可能性:0/0、0/1、0/1或是1/0(斜線前面是「進位」,後面是「和」)。
|
|
| 不考慮進位的1位元加法器 |
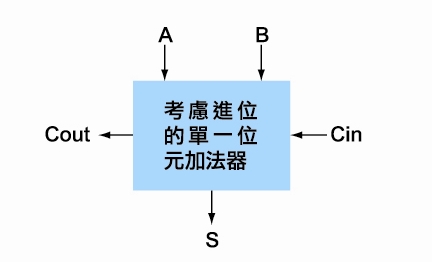
考慮進位的1位元加法器
會有3個輸入(8種可能性,就不列舉了),2個輸出結果(就是「進位」和「和」,也還是4種可能性)。
|
|
| 考慮進位的1位元加法器 |
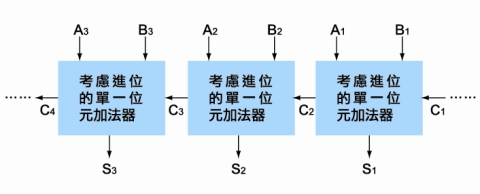
最有意思的地方在於,要「延長長加法運算的位數」,很簡單,只要把「考慮進位的1位元加法器」串連起來就好啦!
|
|
| 想像中的超長位元加法器 |
電腦產品的產生流程
以前的人花了很多的時間、精神,才把問題簡化到這種程度,設法做出加法電路出來。只是,只能做加法的話,看起來我們離「做出一顆處理器」的路還很遠。
這個加法電路還有很多問題,像是,「考慮進位的加法器要如何設計?如何製造?」「這個加法器速度很慢吧?因為你一樣得從左至右,一個位元一個位元的計算,才能得到最後的結果。」「這是加法,那減法呢?浮點數呢?」老實說,這些問題並非不重要,我也不一定懂,不過各位可以從這些「過程中」了解到,電腦硬體(或是其他產品)的「產生過程」大概像是下面這樣的流程:
從需求產生想法
有人想要製造一臺電腦,可以進行10進位的各種運算,以解放繁瑣的運算工作。
簡化問題
結果發現上述作法行不通,於是聰明的人類改變想法,並發現可以設計只用2進位進行運算的電腦,一樣可以用來模擬10進位演算。
把問題切小並設法解決解決小問題(divide & conquer)
一下子就要做出「加減乘除全都會算的電腦」沒那麼容易,那就先從加法開始,先試著設計「1個位元」的加法器。
把單純的解法組合起來,看是否能解決複雜的問題
然後設法把1個位元的加法器組合起來,做出一個多位元的加法器。
設計、製造、測試
根據前面找尋答案的結果,設計產品並進行製造,然後進行測試,看看產品是否能達成原先的設計目標。就像是,做出一個16位元的加法器,試著做做看算術,觀察能否得到正確的答案。
除錯
若是產品成功,「可以正確又快速得到加法的答案了」,則開香檳慶祝;若是失敗,則重複檢視之前的各種「找尋答案」的過程,設法找出失敗的原因,並移除之。
反覆進行最佳化
就算產品可以運作,也許還是會有各種「不理想」,像是「加法進行得很好,但是不會減法」,或是「加法的速度進行得很慢」,那就還得精益求精,設法解決這些「不理想」的情況。像是「效能問題」、「品質問題」。所謂「世事無絕對──但是絕對還有更好的辦法解決問題」(真是矛盾的說法?)。當然,要不是「有利可圖」,廠商又哪會絞盡腦汁,設法讓產品不斷進步?
因此,我們理解了「加法器的原始想法」之後,接著就是要研究,「如何設計出加法器」。
邏輯運算三元素
事實上,當然,我現在用「倒敘法」講的,就是計算機組織裡面的一門科目,稱為「數位邏輯設計」。這門課一開始就會教你一些基本的原理,其中一個原理稱為「邏輯運算」。邏輯運算中有三個基本運算,分別是「或(OR)」、「且(AND)」和「反(NOT)」。數位邏輯的課本說,「世界上所有的複雜邏輯運算,都可以用這三個基本邏輯運算模擬出來」。所以,我們來介紹一下,這「邏輯運算」是什麼:
OR運算
0 OR 0 = 0
0 OR 1 = 1
1 OR 0 = 1
1 OR 1 = 1
通常,運算式中,有所謂的「運算元(operand)」和「運算子/運算符(operator)」的專有名詞。
在「0 OR 1 = 1」這個算式中,等號前面的「0 OR 1」中的0和1是「運算元」,也有人稱之為「輸入(input)」,中間的OR是「運算子」,就是定義這個運算的主角了,等號後面的1則稱為「結果(result)」或是「輸出(output)」。
「OR」運算就是:只要兩個輸入中其中一個有1,輸出就會有1。
AND運算
0 AND 0 = 0
0 AND 1 = 0
1 AND 0 = 0
1 AND 1 = 1
「AND」運算就是:只有兩個輸入都是1的時候,輸出才會是1。
NOT運算
NOT 0 = 1
NOT 1 = 0
「NOT」運算是個「單運算元」的運算子,也稱為「反相運算子」,0被反相就變成1,1被反相就變成0。
一般在數位邏輯課本中,會用三種圖樣來表示這三種邏輯閘,並加註所謂的「真值表」: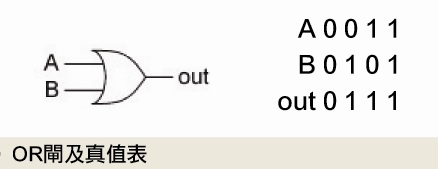
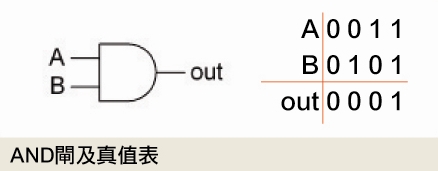
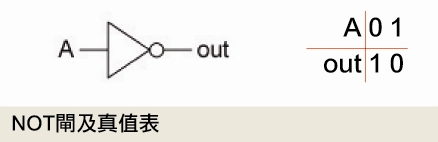
假設我們能製造出這三個基本邏輯閘,就可以用他們模擬出所有可能的邏輯運算。然後,用邏輯運算,又可以模擬出人類定義的數學運算。所以,下期就可以用這期學到邏輯閘概念來模擬做出加法器了。
熱門新聞
2026-02-02
2026-02-03
2026-02-04
2026-02-02
2026-02-04
2026-02-03
2026-02-05