【moda專欄】電子簽章的相關技術介紹

作者／數位發展部資訊處 周智禾副處長

近期為因應資訊科技及數位經濟的迅速發展，我國正如火如荼展開相關電子簽章法修法作業。本篇將深入探討其中的技術細節。

與《電子簽章法》修法相關討論，請參考這篇文章：電子簽章法新制與產業新興應用場景

什麼是電子簽章？

我們這裡要探討的是符合《電子簽章法》所定義的電子簽章（Electronic Signature）：指的是依附在電子文件內並與文件相關連，用以辨識及確認電子文件簽署人身分、資格及電子文件真偽的簽章；一般電子簽章常使用演算法與資通訊安全技術（相關技術詳本部 111 年 12 月 2 日產經字第 1114000229 函釋），以達成符合電子簽章法的要件。

其他像是將一張手寫簽名的圖片加到電子文件中，或是在電子文件上，使用手機、平板或手寫板進行簽名等，這些方式容易被人使用繪圖工具進行複製或修改，而不易辨別其真偽，難以正確舉證簽署人的身分，並不是電子簽章法中所說的電子簽章，所具備的效力較低。

我們將使用電子簽章的過程分為三階段來看：

一、事前準備：

使用者選擇線上簽署平臺，如中華電信快意簽、凱鈿行動科技點點簽、蒙恬科技好好簽、臺灣網路認證的 TWES 電子簽署等平臺，先進行註冊及上傳待簽署的電子文件，並指定簽署人資訊、身分驗證方式及待簽章欄位等資訊，以「設定簽章與電子文件的關連」；等設定完成後，簽署平臺會通知簽署人登入平台上進行後續的文件簽署。

二、事中簽章：

當簽署人要在文件上簽章時，會需要通過指定的驗證方式（像是帳號密碼、SMS 簡訊密碼、一次性密碼 OTP 等），來達成「辨識及確認簽電子文件簽署人身分、資格」的要件，然後執行簽章動作，例如將自己簽名的圖片檔擺放到文件中的簽章欄位。

三、事後驗證：

拿到經過電子簽章的文件後，任何人都可以直覺判斷這份文件是否具備合法的簽章。

如果在前一步驟進行電子簽章時，簽署平臺有搭配使用符合 PDF 軟體，如 Adobe 所列的認可信任清單（Adobe Approved Trust List, AATL）的數位憑證（Digital Certificate）來針對電子文件或稽核軌跡資訊進行數位簽章，那麼使用 Adobe Acrobat 或 Acrobat Reader 軟體開啟已簽署文件時，軟體會協助確認文件是否曾被竄改、數位憑證資訊的有效性等，並在軟體上顯示，藉此更好的達成電子簽章法要件中「辨識及確認電子文件真偽」。

更具效力的數位簽章

在這次電子簽章法修法中，明定數位簽章（Digital Signature）是電子簽章的一種，並且符合以下條件：將電子文件以數學演算法或其他方式運算為一定長度之數位資料，以簽署人之私密金鑰對其加密，形成電子簽章，得以公開金鑰加以驗證，並具憑證機構簽發之憑證者。

從這個條件中我們可以看到幾個重點，依先後順序大概可分為 3 個部分：

我們將使用電子簽章的過程分為三階段來看：

一、我們通常會透過雜湊演算法將電子文件進行運算，然後得到一個固定長度的數位資料，除有效縮短資料長度外（一般我們可以把運算結果稱為訊息摘要，就像是用指紋來代替某個真實的人），同時也可以用來加速後續進行數位簽章的運算速度。

二、在進行數位簽章時，以目前常見技術，我們通常使用非對稱式加密系統，每個人會有 1 把公開金鑰及 1 把私密金鑰，要進行簽章的人（稱為簽署人），會用他的私密金鑰（就像是他的私人印章）對前面固定長度的數位資料進行加密運算（就像蓋章的動作，在密碼學中實際稱為簽章運算），其結果稱為數位簽章。

三、任何人拿到前面的數位簽章，如果想要驗證這個數位簽章的正確性，可以拿簽署人的公開金鑰進行驗證，為了知道這把公開金鑰是不是真的是屬於這個簽署人的，我們會拿憑證（就像是印鑑證明）來證明它的真偽。

這雖然聽起來很複雜，但對簽署人來說其實完全可以對應到現實生活中經常使用的簽名需求：假設我們要簽署一份文件，只要使用自己的個人私章（私密金鑰）進行蓋章（簽章），就可以得到這份蓋章（簽章）後的文件，若要確認蓋章（簽章）的真實性，只需要利用蓋章人的印鑑證明（簽章人的公開金鑰）進行驗證即可。

在真實世界中，我們可以透過申請得來的印鑑證明來確認印章的真實性及正確性，但在數位世界中，前面所提的數位簽章過程有一個問題：如何得知拿到的公開金鑰是正確的？畢竟它看起來只是一串很長的數字或是英數混合的字串。這時候就需要一份資料能夠說明和證明這把公開金鑰是誰的，這份資料就是所謂的「憑證（Certificate）」。憑證的內容包含序號、版本、公開金鑰、用途（用來加解密或簽章）、識別碼、有效日期等資訊，但這些內容只能說明這張憑證是誰的，並不能保證憑證是真的，所以需要有一個公正第三方來為這張憑證進行背書，也就是憑證機構（Certificate Authority, CA）。

像是中華電信通用憑證管理中心（PublicCA）及台灣網路認證公司（TWCA）皆為憑證機構，而背書指的是「由憑證機構為這張憑證進行簽章」，因此簽章還包含簽發者名稱、簽發者唯一識別碼、簽章演算法、CA 對這張憑證的簽章等資訊，可以確保這張憑證的完整性及不可否認性。

總之，這次修法特別強調數位簽章能「連結及識別簽名人」、「偵測簽名所依附文件之改變」，並且「具憑證機構簽發之憑證，具一定程度的公信力」，因此「推定」為本人親自簽名或蓋章的效力。

接下來我們將近一步解釋數位簽章的技術細節及相關的名詞。

淺談密碼學

前文我們解釋了數位簽章需要以私密金鑰進行數學的運算，但實際上怎麼進行呢？這牽涉到一些密碼學（Cryptography）的相關知識。讓我們先有個簡單的概念：加密前的訊息稱為明文（Plaintext），而加密後的則稱為密文（Ciphertext）。

對稱式密碼系統

早在上千年以前就出現著名的凱薩密碼（Caesar Cipher），其原理是將明文的每個英文字母使用往後數的第三個字母來取代，例如把 A 用 D 取代、把 B 用 E 取代，以此類推，全部取代完後的訊息就是密文；之後也出現多個類似用這種取代（Substitution）技巧，而複雜度越來越高的密碼系統。

另一類密碼系統則是使用置換（Transposition）的技巧，主要是將明文的每個字母按一定的規則進行重新排列成為密文，例如明文為digitalaffairs，把它分成 2 行寫，再按列的順序讀取成為密文，如表圖 1 所示。

表圖 1：使用置換技巧之加密方式（圖片來源／數位部）

你會發現，前面所提到的取代或置換，只要你知道明文如何轉換成密文的規則，你就可以很容易將密文再轉回原本的明文，這個規則如同一把金鑰（Key），只要反過來執行一次就行了。

這就是對稱式密碼系統（Symmetric Cryptosystem），加密及解密使用同一把金鑰。隨著時間的推移，密碼系統透過更複雜的取代及置換，再搭配其他數學邏輯（如「互斥或」Exclusive or, XOR）或其他運算等，形成更加安全的對稱式密碼系統，簡單的示意如圖 2，如近代著名的資料加密標準（Data Encryption Standard, DES）、進階加密標準（Advanced Encryption Standard, AES）等。

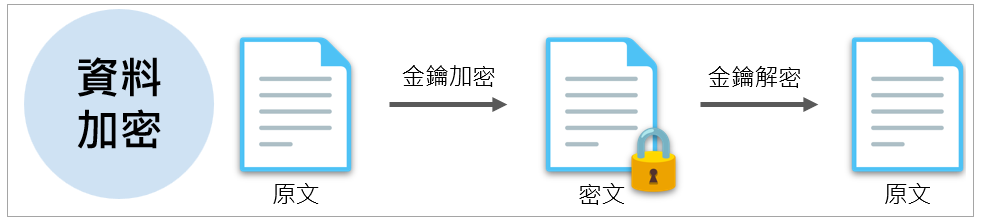
圖 2：對稱式密碼系統加解密（圖片來源／數位部）

對稱式密碼系統成功實現了我們對資料機密性的需求，它的優點包括，金鑰較小：金鑰長度如果是 128 位元，把它轉成我們生活常見的十進位數字，長度大概是 38 位數，而適用於缺乏運算能力的環境；此外，對稱式的加解密機制容易使用硬體來實作，執行速度相當快；最後，它還能有效抵抗這幾年大家常討論量子運算（Quantum Computing）所帶來的破密威脅。

但因為它的機制是加密及解密使用同一把金鑰，因此衍生出諸多問題，例如，通訊雙方彼此不認識，如何產生或分享同一把金鑰？此外，每個人都要與另一個人之間有一把獨一無二的金鑰，將會造成金鑰數量龐大，例如有 1,000 個人，彼此之間都有加密解密的需求，那麼任兩人之間都要有一把金鑰，透過排列組合運算，總共需要 C10002 把金鑰，也就是 499,500 個；最後，因為通訊雙方都有同一把金鑰，我們無法得知是誰拿金鑰對訊息進行加密，無法滿足不可否認性（Non-Repudiation），也就是說，你無法確切知道是誰拿金鑰對訊息進行加密運算，萬一這把金鑰不小心掉了，也無從知道是誰洩露了。

非對稱式密碼系統

因為對稱式密碼系統存在許多尚待克服的議題，因此後面發展出非對稱式密碼系統（Asymmetric Cryptosystem），如 RSA、橢圓曲線密碼學（Elliptic Curve Cryptography, ECC），這也是目前數位簽章主要的使用技術。

非對稱式密碼系統與對稱式密碼系統最大的不同點在於，每個人都會有 2 把金鑰，分別為公開金鑰（Public Key）及私密金鑰（Private Key），使用者先選擇一把私密金鑰並收藏好，不讓別人知道，之後就可以輕易地計算得到相對應獨一無二的公開金鑰。

公開金鑰及私密金鑰的用法有兩種，第一種是所謂的加解密，假如 Alice 想要將訊息加密傳給 Bob，那麼 Alice 拿 Bob 的公開金鑰對訊息進行加密運算得到密文，Bob 收到後拿自己的私密金鑰進行解密運算得到明文；另外一種應用則是所謂的數位簽章。在大部分的密碼系統中，加密指的是拿對方的公開金鑰來進行加密運算，而簽章一樣是執行加密運算，只不過改成拿自己的私密金鑰。你會發現，前面所提到的取代或置換，只要你知道明文如何轉換成密文的規則，你就可以很容易將密文再轉回原本的明文，這個規則如同一把金鑰（Key），只要反過來執行一次就行了。

舉例來說，Alice 想要傳遞一份他看過且認可的訊息，如同現實生活中我們簽署同意書或契約書一樣，那麼 Alice 可以拿自己的私密金鑰對訊息進行簽章運算，運算完的結果就是所謂的數位簽章，任何人想驗證這個數位簽章的真實性，可以拿 Alice 的公開金鑰來進行解簽章運算，解完後的結果再與原始訊息比對是否一致。簡單的示意如圖 3。

附帶一提，前面所談的簽章，一般實務上會先將訊息進行雜湊運算1得到雜湊值，之後再針對雜湊值進行簽章運算，除了可縮小訊息的大小，也可以加快運算速度。

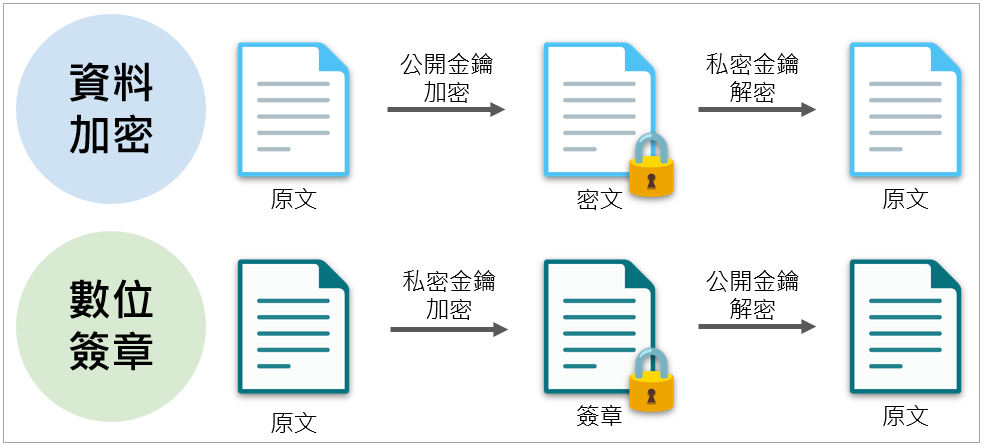
圖 3：非對稱式密碼系統加解密及數位簽章（圖片來源／數位部）

非對稱式密碼系統似乎完美解決了對稱式密碼系統面對的金鑰分配問題，也可透過簽章達到不可否認性，因為簽章需要拿自己的私密金鑰，也只有簽署人有這把私密金鑰。不過，非對稱式密碼系統的公開金鑰及私密金鑰長度相對較長，以 RSA 1024 為例，把它轉成我們生活常見的十進位數字，其長度大概是 308 位數，比起對稱式密碼系統金鑰多出許多，再加上大部分非對稱式密碼系統設計原理是基於特定數學的困難度，計算過程相當複雜，所以它的加解密速度較慢，較難適用於缺乏運算資源的環境。

安全與強度

以下補充幾個非對稱式密碼系統議題。首先是私密金鑰很重要也很隱密，最方便的作法是將私密金鑰儲存成一個檔案，並輔以用密碼保護它，當要開啟及使用私密金鑰時，使用者需要輸入正確的密碼才能使用；另一種常見的作法係將私密金鑰存放到硬體載具中，如自然人憑證，為確保其安全性，私密金鑰不會被讀取出來，所有使用私密金鑰進行解密或簽章時，是將密文資料送到自然人憑證中進行運算，再取得運算完的結果。

此外，非對稱式密碼系統讓任何人都可以拿到別人的公開金鑰，而公開金鑰跟私密金鑰之間存在一定的關係，由於這是基於數學困難度的演算法，並非不能被破解，關鍵在於時間及成本，最直覺的作法是暴力破解法，一個一個去猜密鑰是什麼，就像猜密碼一樣。

如果以電腦每秒可運算百萬或千萬次的速度去破解，可能需要數百年才能完成；但積體電路存在摩爾定律，也就是相同面積的晶圓下生產同樣規格的 IC，隨著製程技術的進步，每隔 18 個月，IC 產出量就可增加一倍。隨著電腦速度越來越快，再加上各式超級電腦的誕生，破解非對稱式密碼系統的時間逐漸大幅降低，所以我們可以發現，這類非對稱式密碼系統所使用的金鑰越來越長，如 RSA 從一開始的 512 位元變成 1024 位元，現在則是建議至少使用 2048 位元，這數字的確相當大，所以要暴力破解需要非常長的時間，甚至安全等級要求高一點的金鑰會長達 4096 位元。

數位信封

對稱式密碼系統及非對稱式密碼系統各有優缺點，各取兩種系統的長處所開發出來的「數位信封」是目前最新型態的做法：假設 Alice 及 Bob 都各自擁有非對稱式密碼系統的公開金鑰及私密金鑰， Alice 先產生一把對稱式密碼系統的金鑰，再拿這把金鑰對明文進行加密後得到密文，然後 Alice 再拿 Bob 的公開金鑰對前面的金鑰進行加密，形成數位信封（Digital Envelope）；Alice 同時把密文及數位信封送給 Bob，Bob 用自己的私密金鑰對數位信封進行解密以得到金鑰，再用這把金鑰對密文進行解密以得到明文，如圖 4 所示。

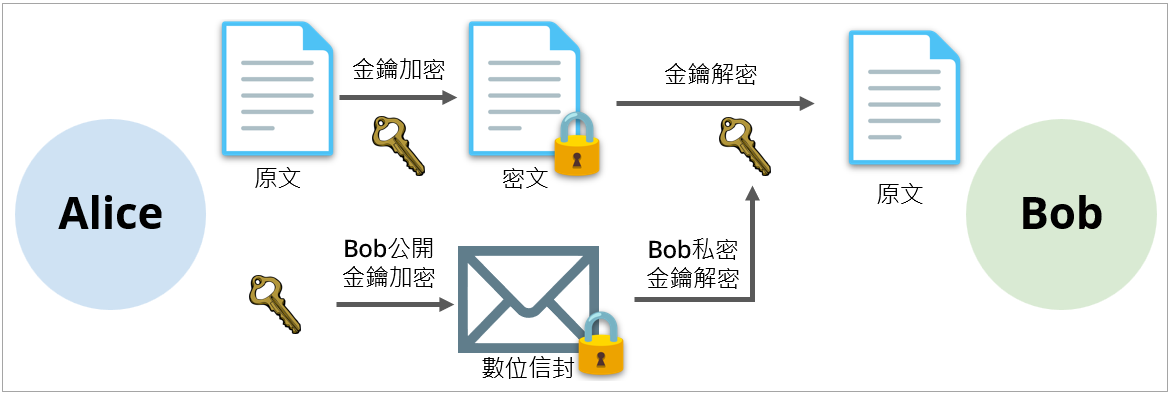
圖 4：數位信封（圖片來源／數位部）

與時俱進的數位簽章

隨著數位簽章的技術成熟，搭配本次修正電子簽章法，確認使用經主管機關許可的憑證機構所簽發的憑證，除強化數位簽章的效力，並要求各行政機關須以法律明定排除電子簽章法適用，數位簽章將如同傳統紙本時代的印鑑證明，可推定數位簽章為本人親簽或蓋章，在法律訴訟上具有更強的證據能力。未來，現行紙本模式的行政程序，基本都可以採線上方式。

隨著數位簽章的國際標準化及法律認可後，在安全條件相當，且符合國際互惠或技術對接合作原則下，數位簽章可應用在更多國際互動，例如國與國之間簽訂合作備忘錄（MOU），以後將有機會演進成直接進行線上（數位）簽署。

前面提到常用的數位簽章均是使用非對稱式加解密演算法，是目前相對安全的方式，但這類的演算法多是基於數學計算難題（如分解質因數問題、離散對數問題等），未來，運算能力更強的量子電腦可以輕易的破解這些問題。雖然量子電腦目前尚未成熟，但近年來研究機構已開始未雨綢繆，著手研究「後量子密碼學（PQC）」，利用現有的電腦環境，設計出無法被量子電腦有效解決的計算難題，以因應未來可能面臨的威脅。

此外，面對生成式 AI 帶來新的挑戰與衝擊，數位簽章也可以用來驗證資料是否為 AI 或是人類產生，未來數位簽章會是數位世界裡的重要基礎建設，提供信任、驗證與不可否認等機制，值得所有人一起努力，讓數位世界更安全與便利。

（本文轉載自moda blog）