數字,只是人類發明,用來對應數量的符號。
因此,數字可以用不同形式表示,但是其所代表數量的抽象意義是相同的。例如常見的羅馬數字I、II、III、IV、V……,其實和一般的阿拉伯數字1、2、3、4、5……,或是國字的壹、貳、參、肆、伍……,都是一樣的意思。
只因為人類有10根手指頭
既然如此,且讓我們來想想,為何電腦(處理器)只能用「2進位」來做事情?
在解答這個問題之前,請先讓我們來解釋一下「10進位」是什麼。
所謂的10進位,請讓我們看一個簡單的數字:「285」。其中,2是「百位數」,8是「十位數」,5是「個位數」。
用公式表示就是:285 = 2×102 + 8×101 + 5×100。
但是,如果你真的有思考,那我得告訴你,285這符號,僅是為了簡單的描述數量用的符號,事實上,人類也可以把「每一個單一的數量都用一個單一的符號」來表示。
但那會累死人,現代數學就幾乎無法建立了。
如果你夠無聊(至少像我一樣無聊),你從1數到9(1、2、3……9),當你數到「10」的時候,請注意,其實你也可以用一個怪異的符號來代替10(像是,A),這並無損於10的數量意義。只是,10這個符號前面的「1」,實際上我們每個人都知道那其實是「1×101」。如果你硬要用A代表10,行嗎?行,只要你和其他人講話時,人家都聽得懂你說啥就行。你說「魚缸裡有A隻魚」,「我從地上撿到A塊錢」,可以的,只要別人聽得懂就行,只要他知道「原來此時A=10」就可以了。
「電子」是節能快速的基礎
表示數字,基本上是個簡單的事情。但要這些數字做運算,就牽涉複雜多的因素了。以前講過,用「算盤」做數字運算,其實是「人腦」在做運算,但至少算盤簡化了數字的記錄。後來的科學家打算做更精巧的機器,用齒輪、連桿等機械,製造一個「10進位運算機器」。當時的機械製造精密程度不足,因此這類的製造嘗試失敗了。科學家花了很長的時間才了解幾件事:
● 用「機械」的方式製造運算機器,不是不可能,但要做到極端的精密十分困難。
● 製造「10進位」的計算機器也不是不可能,但會造成這機器的設計極端複雜,同樣也幾乎不可能被製造出來。
科學家最後的結論是,「可以製造一臺最省能源、速度最快的計算機器,並且用2進位的設計即可」。
後來這個結論就是「電子計算機」。用電力驅動計算機器,是最省能源的方式(相對於科學家早早就想用的「純機械」的方法來說,電子計算機是超省能源了)。
選擇2進位只是因為「這是必要的」為何選擇「2進位」?
因為,「計算加減乘除」這些運算,事實上都是人類為了處理數量所發明出來的「動作」,這些動作用哪種數字系統來做,結果都是一樣的。選擇2進位只是因為,用來處理運算的「電子計算機」,用2進位的方式(低電位表示0,高電位表示1)來設計是最簡單的方式罷了。
電子計算機(電腦,或是處理器)實際上只是一個「運算的『模擬器』」,選擇2進位只是因為「製造技術上的需求」而已。如果你夠無聊,打算做一臺「3進位的電子計算機」,行嗎?行的,但這3進位的機器能做的事情不會多於2進位的計算機。而2進位計算機所做的任何運算,都可以同等於10進位運算。因為,設計處理器的人會設法讓它「模擬的就像是人類運算一樣」。
這稱為「超越工程學」。
所以,無論是當初還是現在,你就知道:為何學電腦,學處理器,學計算機概論,學院派的教學總是要你去學「數碼系統的轉換」,其實那只是因為:用2進位設計電腦是「目前人類已知唯一的選擇」。會不會火星人其實用9進位來設計電腦?天曉得,雖然不無可能,但你得去問火星人才知道答案就是。
由於可用高低電位來代表0與1,人類便可據此設計模擬一般數學運算的邏輯電路。因此現代計算機科學的基礎,可說完全建立在這種「二進位運算」和「二元性電路」的特性上。幾乎所有的計算機科學相關教科書,也都假設讀的人了解這件事。當然,這個結論可能不是鐵律,你也可以辯稱這種方式的電腦無效率(什麼,只能用二進位?)。不過,到目前為止,所有的商業電腦都是用「電路和數字的二元性」來設計。如果閣下只是想了解電腦,那也暫時別去管為什麼了,先記下來就是了。想了解「為什麼二元性這麼重要」,得慢慢學,學熟了才有點概念。
常用數碼系統的介紹
但是,用2進位的方式,數字的紀錄會過於冗長,因此學電腦,學處理器的原理,我們都得先學「數碼系統的轉換」。
在此介紹一個名詞:基底(base)。
人類常用的數字是10進位,我們通常就說這是以10為基底的數字表示方式。比方說「285」,我們就知道這是二百八十五,2×102 + 8×101 + 5×100。有時候,我們會寫成(285)10,下標的10就是說這數字的基底為10,也就是說「這是10進位數字」。
一個數字可以任選基底來表示,不會影響所表現的數量意義。例如(1111)2 = (15)10。首先現在來介紹一下,一般常見的數碼系統有哪些:
● 2進位:0,1,10,11,100,101,110,111,……
● 8進位:0,1,2,3,4,5,6,7,10,11,……
● 10進位:0,1,2,3,4,5,6,7,8,9,10,11,……
● 16進位:0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,10,11,……
顧名思義,數碼系統是「以2為底」,那就是2進位。逢2進1。而「以16為底」是比較特殊的系統,因為你得用15個不同的符號來代表整個數碼系統,因此「9」後面接的是「A、B、C、D、E、F」,分別代表原先十進位的10、11、12、13、14、15。剛開始,面對數碼系統中夾雜英文,初學者大多不太習慣。不過這也沒什麼,只要看多了就習慣了。
可以有其他不同的進位系統嗎?五進位?十二進位?可以的,選擇任何數當作基底都可以。可是選擇其他的基底並沒有太大用途,相當罕用,我們就不花太多力氣在這方面的說明了。
怪異的符號只是因為他是16進位
不過,我對數碼系統的說明,打算介紹到這裡就好了。大家可以看一下「各種基底數字對照表」,就可以知道,各種基底不同的數字,雖然是表示同樣的數量,但是所謂的符號卻是不同。比方說:你突然看到「10」,但若是16進位的10,其實是等於10進位的16,也就是:(10)16 = (16)10。又或者說,(12)10 = (1100)2 = (14)8 = (C)16。
當你看到Debug裡面的奇怪的符號,其實,只不過,那都是用16進位表示的數字罷了。為何選16進位?因為用2進位表示數字太冗長。那為何一定要用2進位設計處理器?只是因為電子計算機用2進位(電位高低)的方式最容易設計。
本期結語:最後,請熟記「類比」和「數位」的真實意義
講到這裡,我們用倒推的邏輯來想:什麼是「類比」?什麼是「數位」?常聽到有人說「數位計算機」、「數位電腦」,為何不是「類比計算機」?
數位這個詞,其實只是指「用數字來表示數量」罷了。比方說,大多數手錶用指針(所指的角度)來表示時間數量,不是用數字,但是所謂的電子錶就直接顯示數字時間,簡單省事直接。
換句話說,「類比」是所謂的「依類相比」,為了表示數量,你得有個依據,用角度,用其他的物件,用繩結,用各種適合的東西來表示數字,都是類比。而「數位」只不過是用類比方式表示出來的數字本體罷了。
事實上,世界上只有類比的數字表示方式,沒有什麼絕對的數位化數字表示方式。
「這很怪哩!」
但就是如此。
手錶上的數字,實際上也是由晶片的電子訊號記錄並顯示,電子訊號就是類比的訊號(電位高低)。光碟上的訊息,是用溝槽的高低變化記錄的,這「高低變化」就是類比的。硬碟上的訊息,是用磁極的南極北極記錄的,磁極的南極北極就是類比的。
懂了這概念,你接下來的處理器理解之路,又邁進了一大步。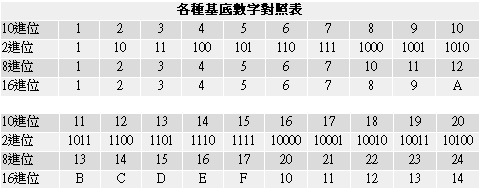
熱門新聞
2026-02-06
2026-02-09
2026-02-06
2026-02-09
2026-02-06
2026-02-06