請再次複習「超越工程學」。一般工科的大學生在學電腦科學的「邏輯設計」時,應該已經得知這樣的推理過程了:
● 可以用「數位電路」模擬「邏輯運算」
● 可以用「邏輯運算」模擬「數學運算」
● 可以用「數學運算」模擬「各種可能的演算應用」,像是「影片播放」、「3D特效」等等
所以,整個「數位邏輯」的課程都在教這些事情(用這個模擬那個)的細節(方法和原理)。因為「魔鬼都在細節裡面」,所以這課程還不太容易懂。但是,就難度而言,其實數位邏輯的內容已經算是蠻簡單的(和傳統的類比電路相比,數位電路起碼不會太虛無縹緲)。而現代處理器的原理,其實就是這種「模擬器」的本質而已。幸好,我們不是學生,不用管這些細節。
這期,我們將要研究怎樣做出一個「不用考慮進位的加法器」和「考慮進位的加法器」的方法──用上期教的邏輯閘來模擬就可以了。
位元的定義
為了避免讀者不清楚專有名詞而導致誤解內容,這期先簡單定義一些單位。
位元:俗稱bit,是2進位世界中用來表示資料的最小單位。通常1位元(或是1-bit)只能表示兩種狀態中的一種:0或1。
位元組:俗稱byte,因為bit單位真的太小,所以通常以1-byte = 8-bit來表示資料。雖然這並非「一定」,你也可以說1-byte = 4-bit,但這種用法因為太罕見,所以目前大家都以1-byte = 8-bit作為資料容量的基本單位。
字組:俗稱word,請注意這個word不是Microsoft Word那文書處理軟體,這word和bit、byte類似,也是電腦內部常用來計算資料容量的一種單位。雖然通常1-byte = 8-bit,但是處理器一次可以處理多個byte的資料,所以就有人發明了word這樣的單位。早期所謂的「16-bit處理器」,像是8086、80286,它們的1-word就等於16-bit(2-byte),現代32-bit處理器,像是早期的Pentium、Pentium II……,一直到早期的Pentium 4,它們的1-word卻又等於32-bit。到了近代的Core 2系列,AMD的Athlon 64系列處理器,1-word又等於64-bit了。
總之,word一般而言是指「處理器一次所能處理的最大資料寬度」,所以會因處理器而異。
有時候還有所謂的double word(DW)、quad word(QW),就是更寬的資料寬度,這些都是用來描述存資料用的單位。
目前我們把心力集中在「位元」即可。
只能處理兩個2進位數字相加的半加器
把單位的概念記住之後,現在我們來研究「加法器」。在2進位世界裡面,一個位數就是一個位元,一個bit,0或1。
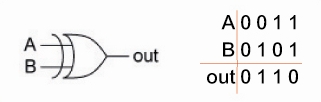
要設計2進位數字的加法器,上期講過,假設用A和B代表輸入,S表示結果(sum,和),C表示進位(carry),那我們可以做出一張表格:
這張表格稱為真值表。用這真值表可以設計出加法器。
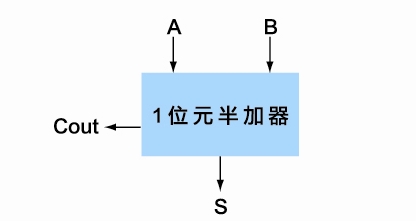
這裡要介紹的這種加法器,其實在數位邏輯課程裡面有個特別的名字,稱為「半加器」。稱為半加器的原因是:它會產生進位,但在「加的動作」部分,它只能做兩個1位元相加,還沒有考慮應該加進去的,從較低位元部分傳過來的「進位」。
這部分,我們就跳過「原理」而直接給你結論。如果各位學過數位邏輯,從上面這張真值表可以得到下列邏輯運算式:
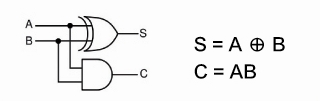
S = A’B + AB’
C = AB
其中,這裡的加號(+)代表的是數位邏輯的OR(A+B其實是A OR B的意思),省略的乘號則是代表數位邏輯的AND(AB其實是A AND B的意思)。而A’或是B’,則表示NOT(反相)的意思(A’就是NOT A)。根據這運算式和上期教過的邏輯閘,我們可以畫出半加器的電路圖: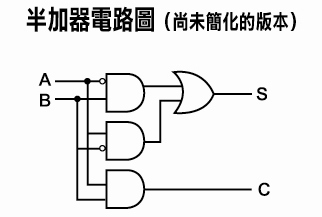
但是,其中的「A’B + AB’」這個算式,因為常用且常見,所以在數位邏輯中發明了一個符號來代表,稱為XOR(中文稱為「互斥或」)。「當輸入不相同時結果為1」,符號則寫作⊕。
|
|
| XOR閘及真值表 |
所以,導入XOR的概念,半加器可以簡化如圖:
|
|
| 1位元半加器電路圖(利用XOR閘簡化的版本) |
|
|
| 1位元半加器示意圖 |
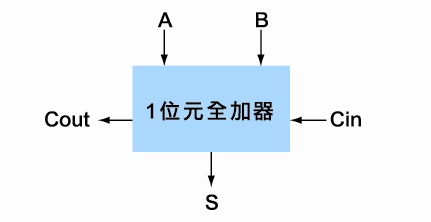
可以做三個2進位數字相加的全加器
但是,人類的算術就是得考慮進位,所以半加器通常只是用來「練習」罷了,用處很小。要設計處理器,我們得從設計「全加器」入手。
請參考全加器的真值表: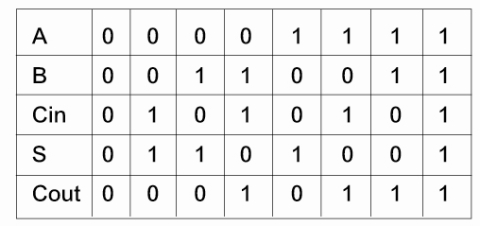
然後,我們可以得到算式為,S = A’B’Cin +A’BCin’+AB’Cin’+ABCin。經過適當的簡化,恰好變成S =(A ⊕ B)⊕ Cin。至於進位的部分,則可以得到Cout = AB + BCin + CinA。這部分,我也沒仔細講解,因為我想那也不是很有趣的部分,也真的需要數位邏輯的基礎。總之,聰明人已經找到了「學理上的基礎」證明了算式是正確的。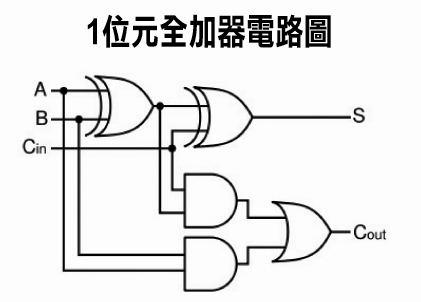
|
|
| 1位元全加器示意圖 |
漣波進位加法器
做出一個位元的全加器以後,事情就好辦了。
如果把全加器連結起來,某種程度上是很省事的。只要我們夠努力的連接,我們可以得到漣波加法器(ripple adder)。稱之為「漣波」,是因為你得從低位元運算到高位元,一個位元算完,再算下一個,有效,但是很慢!這種運算行為,有點像是漣漪的擴散,所以稱為漣波進位加法器。不過,說老實話,人類的算術不也是從低位到高位,慢慢的算上去?除了心算的天才,一般人也都只是這樣算術的吧!
但是,老實說,才沒有哪個處理器現在還用這種原始的想法去做加法器哩!這只是用來做教學的簡單範例。如果你真的去學數位邏輯,書裡面大概都會提到,工程師還發明了運算速度更快的設計,像是「carry look-ahead adder」這樣的設計。
硬體工程師成天想的就是這些。
先有個原始構想,設計線路,然後發現線路不夠快不夠好,於是想辦法調整、改進(當然,也有可能是先出貨,然後在新產品上做調整)。
「真正理解」並「時時回想」
好的,如果各位真的對設計處理器有興趣,各位可以去買一些數位邏輯的教科書來看看。我的簡單硬體教學,大致就講到這邊。總之,結論就是:用數位邏輯設計,就可以設計出各種我們需要的運算線路,達成各種運算目的。
在本期的最後,又要建議各位,學習東西的時候,時時刻刻要休息一下。幹麼呢?停下來,回想一下,「關於過往的學習,是否能夠『連貫』?」
順序來看,半導體開關可以用來製造邏輯閘,邏輯閘可以用來模擬邏輯運算,邏輯運算可以用來模擬數學運算,數學運算用來進行各種演算,這其實是人類跌跌撞撞,摸索出來的設計處理器最佳途徑。過程中,人類曾經想要做出以10進位為基礎的機械計算器(差分機?分析機),在嘗試過各種可能後,才找到這些方法的。再以硬體而言,早期的硬體效率不高,後來才漸漸研究出各種最佳化的方法,現代處理器才會這麼複雜。因為硬體設計師永遠還得找「更好的設計」,試圖把中間隱藏的「延遲」給移掉,硬體工程師想破了頭,「白頭搔更短,渾欲不勝簪」,就是因為他們一直找途徑設計更快、更有效的線路。
對我而言,我以前在學這些東西時,老實說,我是學得很心虛的。
為何心虛?因為,當時我學數位邏輯……為甚麼學?不是很懂。當時學電子電路學,學邏輯閘,為甚麼需要學?不太明白。整體而言,我的心得是:不管你學哪一種學問,中途停下來,問問自己知不知道這東西在你學習系統中的「綱要和定位」,是很有必要的。搞清楚這件事,你才能豁然開朗,「喔,原來數位邏輯的學習必要,是因為:我們不可能製造(真的)會做加法的機器,但我們可以做出會做邏輯運算的機器。這樣的話,我們就可以用邏輯運算器模擬加法了。」
可惜,這些我當時都不太懂。
本期結語:人工智慧是多麼的難以實作啊!
最後,我想再次說明,人工智慧為何難以實作。
其實,人腦和電腦,某種程度雖然有點類似,但那僅只於,我們設計電腦(處理器),只是用來模擬人類的某些運算罷了。倒不是人類不想設計更具人工智慧的電腦,而是……人類根本就沒法發明出那種東西。
想想,連一個簡單的加法,到現在為止,人類都還只是用「邏輯運算」去模擬的,各位以為處理器真的「理解」加法?沒有的,各位想多了。
所以,人工智慧的困難在於,一般人的想像是:也許有一天人類真的會發明出類似人腦的機構。事實上,這很困難,目前的人工智慧和一般人的想像差很多。很多所謂的人工智慧,事實上只是複雜的「知識庫」,用查詢的方式,或是用複雜的程式來幫助人們做決定。離我們想像的,那種好萊塢式的人工智慧,我想至少有十億七千里的距離。
如果你覺得電腦很笨?不,你太看得起它了,它只是個機器罷了,而且它的運作原理比你想像的還更原始多了。如果想要它有智慧,充其量那只是某些人設計的複雜程式而已。所以,放心,天網不會射飛彈到你家,但是恐怖份子就不一定了。
熱門新聞
2026-02-09
2026-02-06
2026-02-06
2026-02-06
2026-02-06
2026-02-06